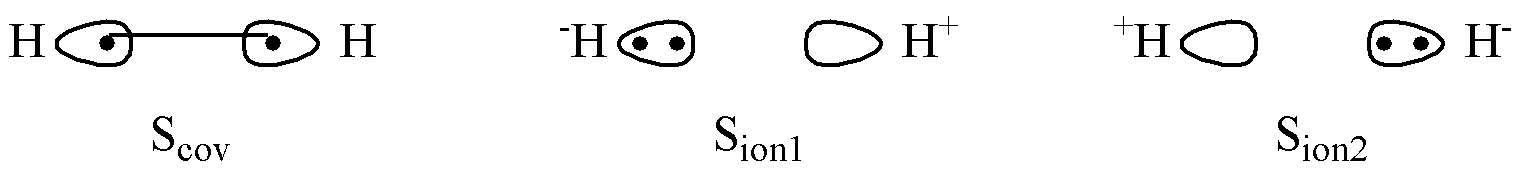2. 价键结构

我们将在这一讲中介绍价键结构的相关概念，了解什么是价键结构，以及如何为一个给定体系产生价键结构。

在开始今天的内容之前，请大家思考一下：

思考

H2 有几个价键结构？1,3-丁二烯呢？更复杂一些，萘呢？O2 分子呢？

2.1. 活性空间

让我们先回到分子轨道理论。分子轨道理论的基础是 Hartree-Fock（ HF ）方法。在 HF 方法中，分子的波函数由单个 Slater 行列式描述，电子依据能量最低原理、泡利不相容原理和洪特规则占据分子轨道。当电子从低能级轨道向高能级轨道激发，就产生了激发行列式，如 图 2.1.1 所示。

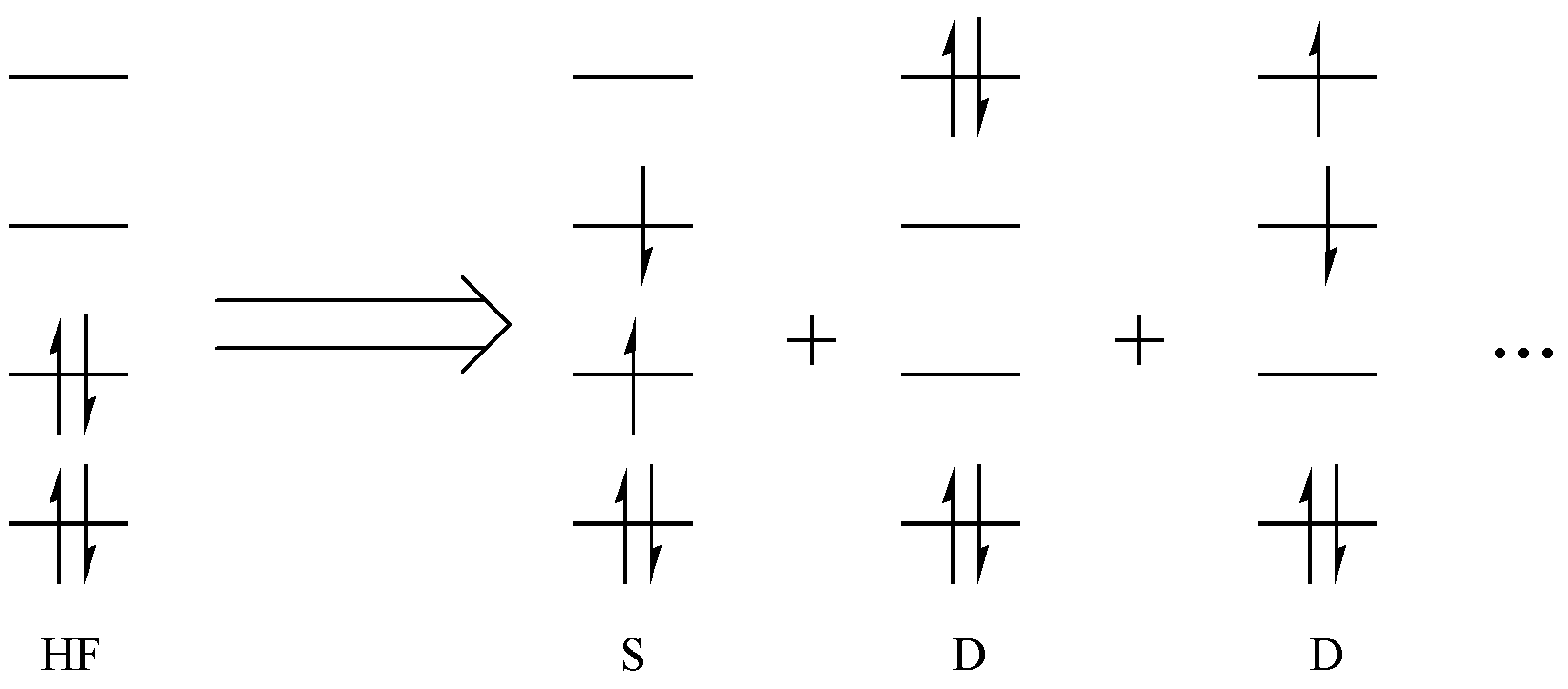
_images/excitation.png

图 2.1.1 从 HF 波函数产生激发行列式

如果只有一个电子产生激发，就是所谓的单激发（ S ）；如果有两个电子激发，就是双激发（ D ）。以此类推，对于一个 n 电子体系，最多会有 n 级激发。如果我们将所有的 n 级激发全都考虑进去，然后求解总波函数，就是完全组态相互作用（ Full CI, FCI ）方法。FCI 方法是公认的最精确的方法，只是这种方法计算量太大，只有少数简单体系可以进行 FCI 计算。于是，化学家们退而求其次，针对体系激发的特点，对于某个化学问题，只允许一部分电子在一部分轨道间进行完全激发。这一部分电子和轨道就被称为 活性空间 ，相应的电子和轨道分别被称为 活性电子 和 活性轨道 ，如 图 2.1.2 中红色部分所示。相对应的，剩余的占据轨道和电子不参与激发，在激发过程中保持不动（占据状态不变），称为 非活性空间 ，如 图 2.1.2 中的蓝色部分。

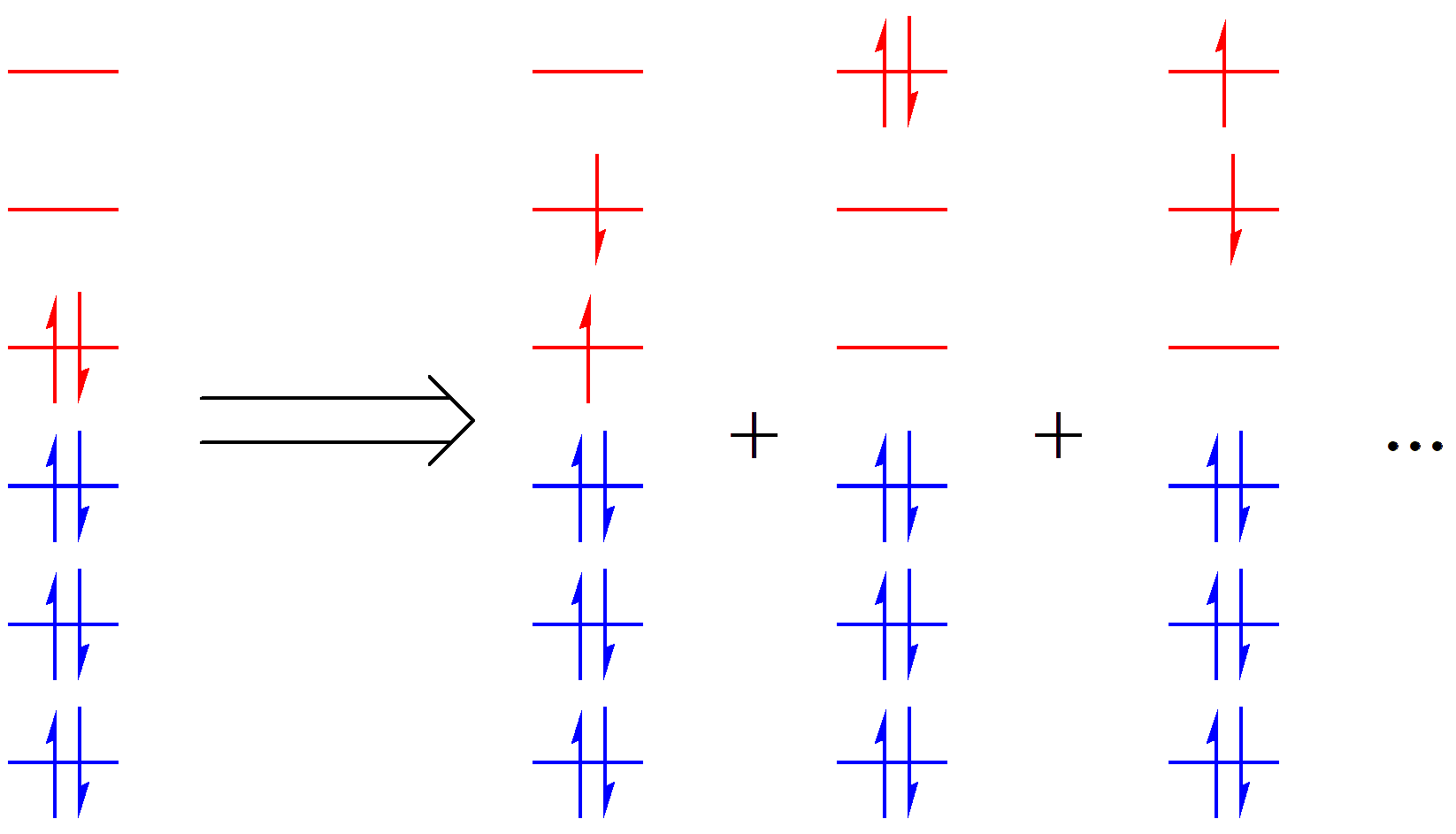
_images/active_space_mo.png

图 2.1.2 分子轨道理论中的活性空间表示

价键理论中的活性空间和分子轨道类似。在价键理论中，依据电子在价键轨道中的不同占据，我们可以得到一系列价键结构。我们针对特定的体系和化学问题，只选取与化学问题有关的价键轨道和对应的电子来产生价键结构，这部分轨道和电子就称为 活性空间 ，如 图 2.1.3 中 C2 H6 分子价键结构中的红色和蓝色部分分别表示活性和非活性空间。

_images/active_space_vb.png

图 2.1.3 价键理论中的活性空间表示

活性空间一般用 (m , n) 来表示，其中 m 表示活性电子数， n 表示活性轨道数。比如， (2,2) 表示 2 个活性电子和 2 个活性轨道； (8,6) 表示 8 个活性电子和 6 个活性轨道。需要注意的是，非活性空间永远是闭壳层。因此，对于含有未成对电子（自旋多重度大于 1 ）的体系，未成对电子和相应的轨道也需要包含在活性空间内。

活性空间是一个非常基础也非常重要的概念。不仅仅在价键理论中，分子轨道理论中的多组态自洽场（ MCSCF ）方法，如完全活性空间自洽场（ CASSCF ）和限制活性空间自洽场（ RASSCF ）等方法中同样也需要活性空间来指明电子激发的数量和范围。

2.2. Rumer 规则

现在，我们已经知道了活性空间的概念。那么，对于一个体系（如一个分子），当指定了活性空间，我们需要如何产生所需的结构呢？

比如，对于 H2 分子，我们可以选择 2 个活性电子和 2 个活性轨道的方案，这样我们就可以得到下图的 3 个价键结构：

这个是非常直观且自然的。对于HF、F2 、C2 H6 等体系，只要我们选取的是两个原子或基团中的单键，我们都可以得到类似的 3 个价键结构。那么，如果是更复杂的情况呢？

对于 1,3-丁二烯（ C4 H6 ），它的分子结构如下：

_images/c4h6.png

假设活性空间是 4 个 \(\pi\) 电子和对应的轨道，我们如何获得所有的价键结构？ 一个最简单的方案就是将所有的可能行都列出来。根据排列组合，我们可以获得相应的 3 个共价结构：

_images/c4h6_cov_wrong.png

图 2.2.1 C4 H6 分子中可能的共价结构

但是，如果你利用这 3 个价键结构进行计算，会发现计算出错了！这是因为这 3 个结构并不是线性独立的。可以证明，S3 可以表示为 S1 和 S2 的线性组合：

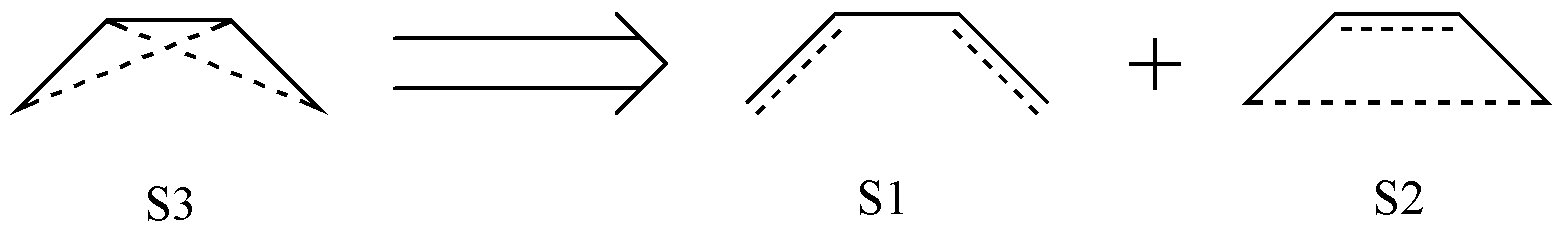
_images/c4h6_cov_linear_comb.png

图 2.2.2 C4 H6 分子共价结构间的线性组合

实际上，C4 H6 分子一共只有 2 个共价结构。因此，我们按照简单的排列组合获得的价键结构其实是有 冗余 的，我们必须要将冗余的结构剔除才能进行价键计算。那么，我们如何识别冗余结构？或者说，我们如何产生 没有冗余 的价键结构？这就需要我们运用 Rumer 规则 来产生价键结构。

2.2.1. 闭壳层情况

我们先来看简单的闭壳层情况。对于闭壳层体系，所有电子完全配对，此时 Rumer 规则产生价键结构的流程如下：

  1. 将活性轨道按一定顺序排列为一圈，并标记序号；

  2. 对于离子结构，确定双占轨道和空轨道的位置；

  3. 对剩余的轨道，按照排列组合两两配对划线，并剔除所有 交叉 的结构，剩下的就是线性独立的结构。

让我们尝试用 Rumer 规则来产生 C4 H6 的价键结构。首先，我们将 4 个活性轨道排列为一圈并标记序号：

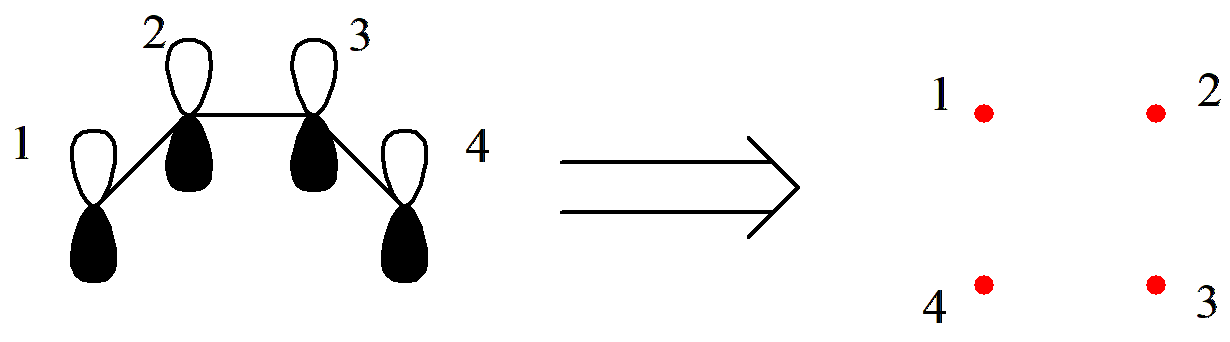
_images/c4h6_rumer_step1.png

图 2.2.3 将 C4 H6 的 \(\pi\) 轨道按顺序排列

对于共价结构，我们直接将 4 个轨道两两配对划线：

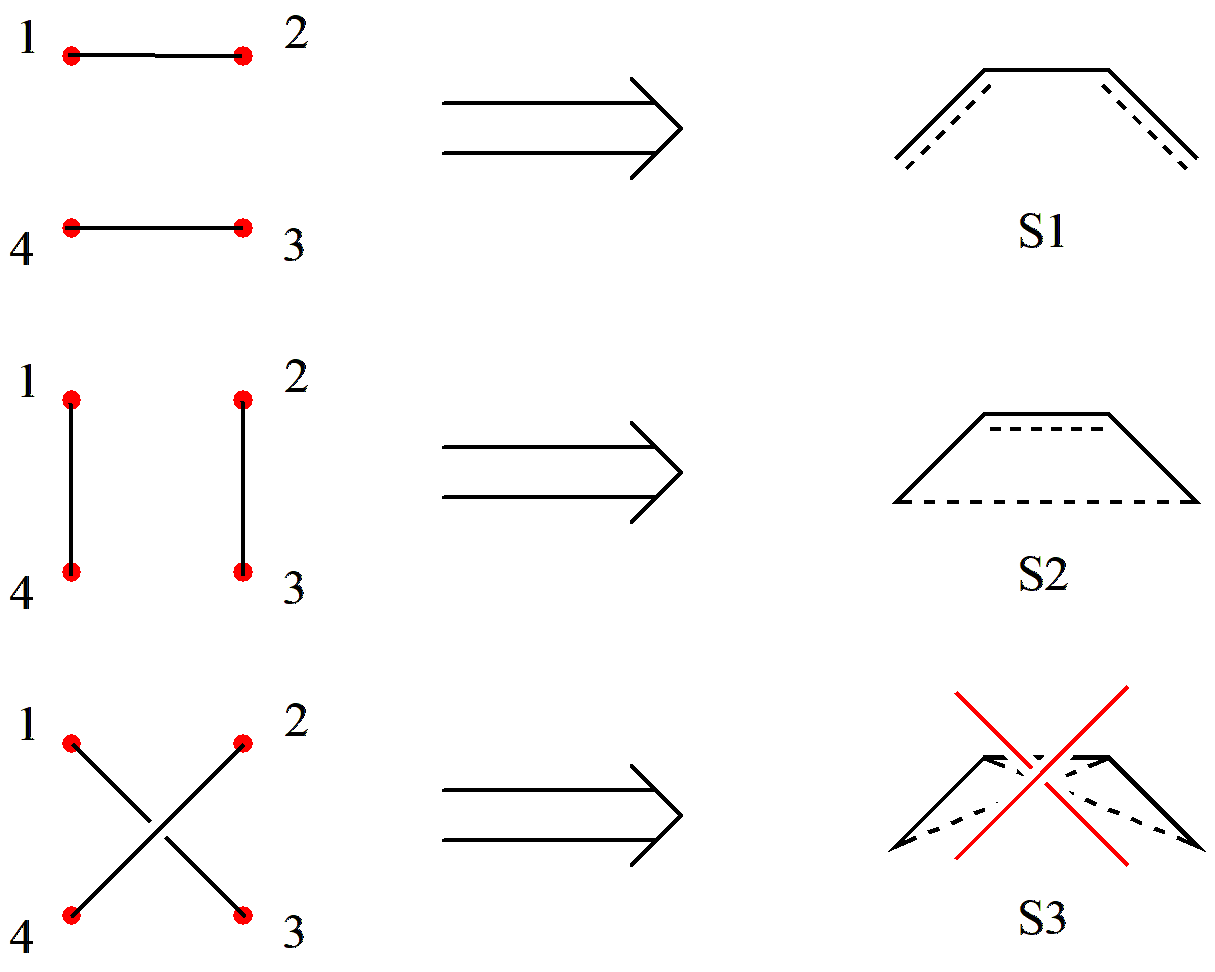
_images/c4h6_rumer_step2.png

图 2.2.4 配对成键，并剔除“交叉”的情况

由于 S3 出现了连线的 交叉 ，因此需要剔除。所以，我们得到了 2 个共价结构。

对于离子结构，假设我们现在有一个双占轨道和一个空轨道（一个离子对），因此我们先要固定离子对的位置。由于离子对不是共价键，因此不受“不交叉”规则的影响，按照简单的排列组合来整理即可。最终，我们可以得到如 图 2.2.5 所示的 20 个价键结构，包括 2 个共价结构（ S1-S2 ），12 个一级离子结构（含有一对离子对， S3-S14 ）和 6 个二级离子结构（含有 2 对离子对， S15-S20 ）。

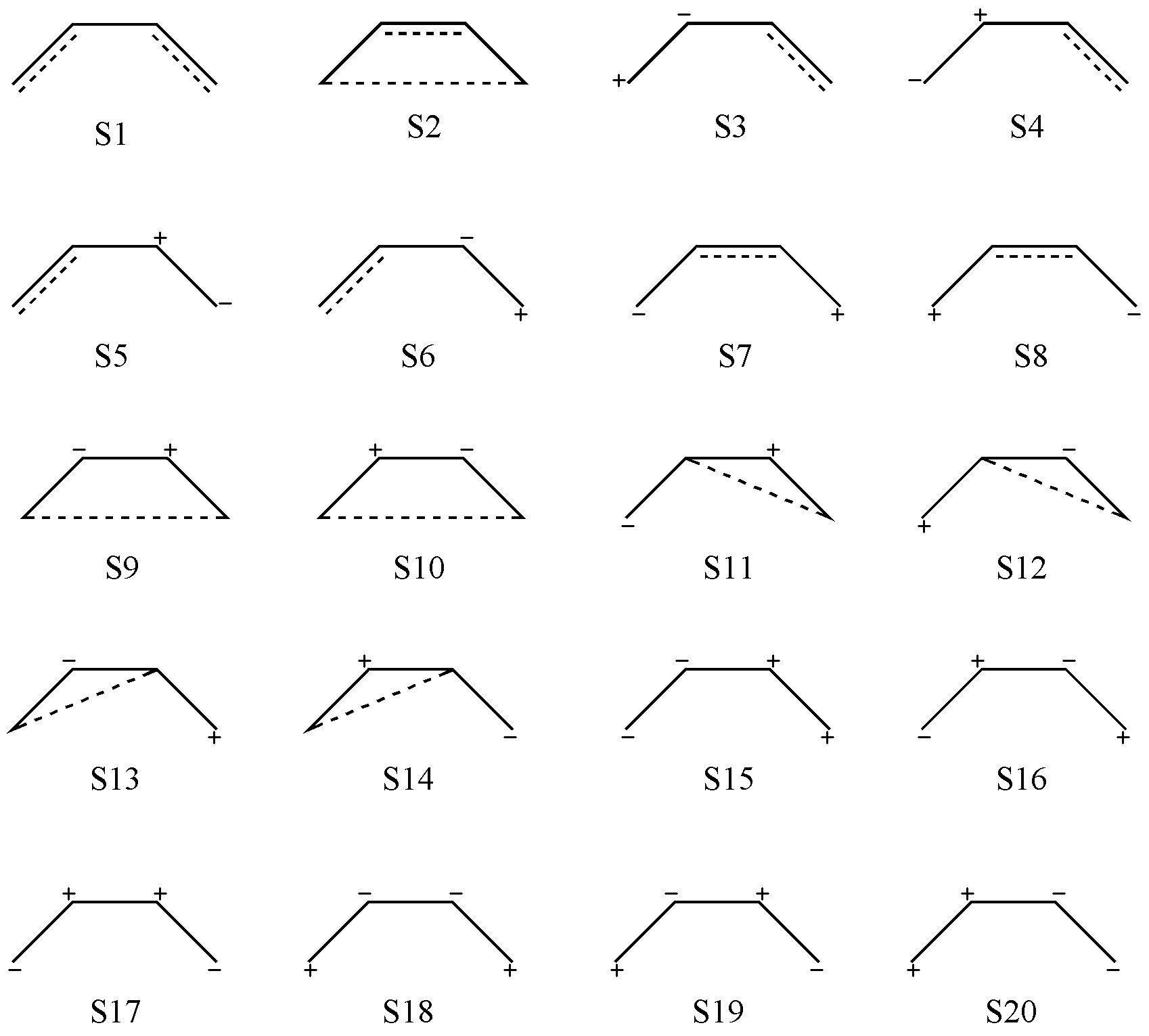
_images/c4h6_structures.png

图 2.2.5 经 Rumer 规则产生的 C4 H6 全部价键结构

2.2.2. 开壳层情况

实际计算中，我们会遇到很多含有未成对电子的开壳层体系，比如各种自由基。对于这类体系，我们需要对闭壳层的 Rumer 规则做一些修改：

  1. 将活性轨道围成一圈时，我们需要多加一个 极点 。

  2. 在连线时，极点只和未成对电子连线，且一个极点可以和多个未成对电子连线；

  3. 共价键既不可以和其它共价键交叉，也不可以和涉及极点的线交叉。

我们再用 C4 H6 的共价结构举个例子。假设此时 C4 H6 是三重态，即有 2 个 \(\pi\) 电子是未成对的。因此，我们第一步画的圈就变成了：

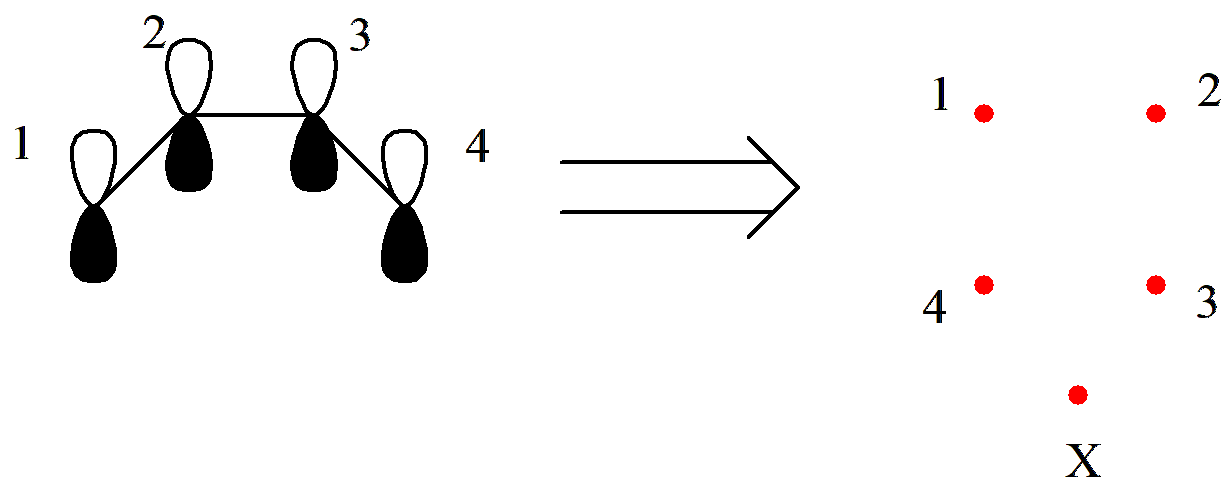
_images/c4h6_rumer_step1_triplet.png

图 2.2.6 三重态 C4 H6 的 \(\pi\) 轨道排列

其中 X 表示极点，用来和未成对电子连线。之后，我们进行连线：

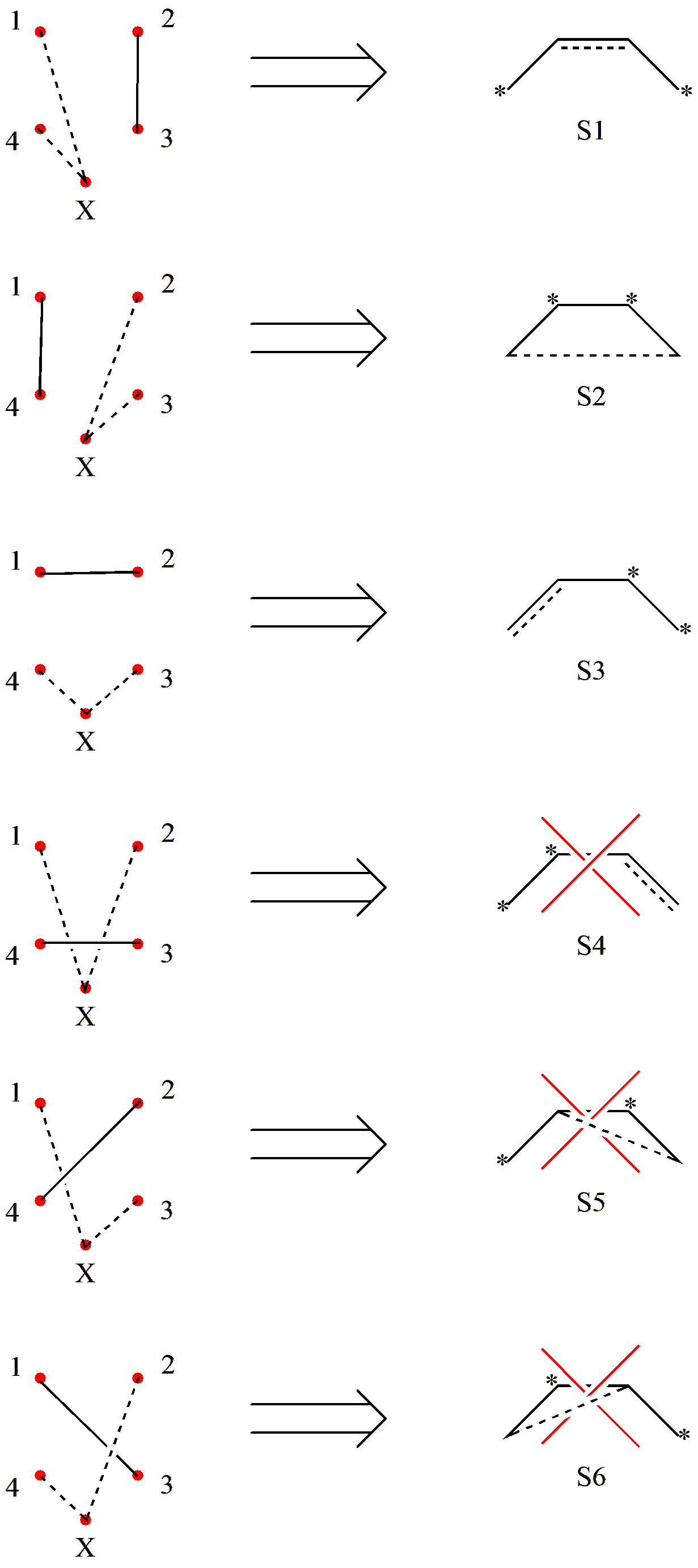
_images/c4h6_rumer_step2_triplet.png

图 2.2.7 三重态 C4 H6 的共价结构筛选

可以看到，虽然我们通过排列组合得到了6个共价结构，但是只有 3 个是满足“不交叉”的要求的。因此，三重态 C4 H6 有 3 个共价结构。同样的，我们可以根据 Rumer 规则得到三重态 C4 H6 所有的价键结构。

练习

请用 Rumer 规则画出：

  1. 三重态 C4 H6 所有的价键结构。

  2. 闭壳层苯分子 \(\pi\) 空间 (6,6) 下的所有价键结构。

  3. 丙烯基自由基（ C3 H5 ) \(\pi\) 空间 (3,3) 下所有的价键结构，结构见下图。

_images/c3h5.png

实际计算中，XMVB 可以根据 Rumer 规则自动产生指定活性空间下的价键结构。大家在这里只需要了解 Rumer 规则的思想就可以了，无需过多纠缠于细节。

2.3. 如何解读 XMVB 中的价键结构？

在 XMVB 计算中，每个价键结构会被表示为一串数字。那么，如何解读这些数字，从而知道我们得到了哪些价键结构？

在 XMVB 中，价键结构的表示以电子对为基础。从第一数字开始，每两个数字表示一对电子的占据情况，数字表示相应电子的占据轨道编号。对于含有 a 个未成对电子的体系（多重度 a+1 ），结构的最后 a 个数字表示未成对电子的占据轨道编号。需要说明的是，价键结构的解读需要结合轨道的定义才能真正完成，因为结构的化学图像依赖于具体的轨道。我们这里先解释价键结构本身的解读，价键轨道的定义以及如何进一步完成解读将在后续章节完成。

我们首先以 H2 为例。H2 是闭壳层体系，所有电子都成对。XMVB 的输出显示，H2 包含以下 3 个价键结构：

1  Number of structures:     3
2
3 The following structures are used in calculation:
4
5       1   *****     1-2
6       2   *****     1 1
7       3   *****     2 2

第一个结构 1-2 表示一对电子，其中一个占据在轨道 1 上，另一个电子占据在轨道 2 上。中间的 - 表示这两个电子配对成键，因此这个结构表示H2的共价结构。结构 1 1 表示电子对的两个电子都占据在同样的轨道 1 上，因此表示一个离子结构。同理，结构 2 2 表示另一个离子结构。

我们再来看一个复杂点的体系，F2 分子。F2 分子也是闭壳层，总共有 18 个电子，活性空间为 (2,2)。简单计算可知，非活性轨道一共有 8 个，非活性电子有 16 个。XMVB 给出的结构信息为：

1  Number of Structures:           3
2
3The following structures are used in calculation:
4
5      1 *****  1:8    9-10
6      2 *****  1:8    9 9
7      3 *****  1:8   10 10

可以看到，每个结构开头都有 1:8 这个信息。在 XMVB 中，这个信息表示有 8 对电子双占，这些电子占据了前 8 个轨道。这种写法等同于 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 。由于每个结构都有这个信息，说明这 16 个电子在所有结构中的占据都是一样的，因此表示的是非活性空间。第一个结构最后的 9-10 表示两个电子分别占据轨道 9 和 10 且配对成键，是共价结构。后两个结构分别表示两个离子结构。

最后，我们来看看 O2 分子的结构解读。由于 O2 的结构比较多，因此我们选取了以下两个结构：

1  1 *****  1:4    7 7    10 10    5-6   8   9
2  2 *****  1:4    8 8     9 9     5-6   7  10

O2 分子是三重态，因此每个结构最后两个数字表示未成对电子占据的轨道。每个结构开头都有 1:4 ，表示前 4 对电子在所有结构中都是双占，因此是非活性空间。第一个结构中的 7 7 10 10 表示两对电子分别双占轨道 7 和 10 ， 5-6 表示一对电子分别占据轨道 5 和 6 并成键，最后轨道 8 和 9 分别占据一个未成对电子。同样，我们可以发现，第二个结构同样表示轨道 5 和 6 之间成键，但是双占轨道变成了 8 和 9 ，未成对电子占据了轨道 7 和 10 。

2.4. 哪些价键结构比较重要？

在价键计算中，我们常常需要判断哪些价键结构比较重要。例如，当我们需要判断化学键属于哪种类型（共价、离子或其它），我们需要了解其中最重要的价键结构。此外，当计算涉及的价键结构非常多的时候，我们常常需要对价键结构进行筛选，从这些价键结构中挑选出一部分价键结构进行计算，而根据价键结构的重要性进行挑选就是最常用的筛选方案。在价键计算中，我们常常使用 权重 作为依据判断结构的重要性。

价键结构 K 的系数 \(C_K\) 可以通过求解久期方程来得到：

\[\mathbf{HC} = E\mathbf{MC}\]

其中 H 和 M 分别为 Hamiltonian 和重叠矩阵

\[H_{KL} = \langle \Phi_K \vert \hat{H} \vert \Phi_L \rangle\]
\[M_{KL} = \langle \Phi_K \vert \Phi_L \rangle\]

其中 \(\Phi_K\) 和 \(\Phi_L\) 表示价键结构 K 和 L 。

在分子轨道理论中，由于轨道正交，结构（组态）之间一定是正交的，因此，权重可以简单地表示为系数的平方：

\[W_K = C_K^2\]

对于价键理论，由于轨道不正交，我们不能简单地用上式来表示权重。此时，权重的定义并不唯一。常用的权重有 Coulson-Chirgwin（CC）权重、Löwdin 权重、Inverse 权重等。

CC 权重是最常用的权重类型，定义直观，计算简便。它的定义如下：

\[W^\textrm{CC}_K = \sum_L{C_KC_LM_{KL}}\]

CC 权重的问题在于某些情况下会出现权重为负数的情况。一般来说，负权重意味着这个结构不重要。Löwdin 权重的定义为：

\[W^\textrm{Löw}_K = \left(\sum_L{C_L(M_{KL})^\frac{1}{2}}\right)^2\]

Inverse 权重的定义为：

\[W^\textrm{Inv}_K = \frac{N_K}{\sum_K{N_K}}\]

其中 \(N_K\) 的定义为：

\[N_K = \frac{C^2_K}{(\mathbf{M})^{-1}_{KK}}\]

这两种权重定义都避免了负权重的产生，但是都需要对重叠矩阵进行求逆或对角化操作，因此计算量比 CC 权重更大。XMVB 中同时给出了以上这几种权重定义的结果，用户可以根据自己的实际需要选取合适的权重。