5. 共振能的计算与应用
在上一讲,我们了解了如何计算解离能。键解离能是一个真实的物理量,我们很容易在现实世界中找到具体的实例并进行观测。这一讲中,我们将介绍一个在价键中非常重要,却很难在现实世界中观测的物理量: 共振能 。
5.1. 共振能的定义
共振能( Resonance Energy,RE )是随着 Linus Pauling 的共振论而提出的。在共振论中,分子的稳定结构是由一系列价键结构 共振 而成的。从波函数的角度看,分子的总波函数表示为各个价键波函数的线性组合。每个价键结构的能量各不相同,其中会有一个或数个价键结构的能量最低,由此在分子的总波函数中权重最大,分子的结构会更多地体现这一个或数个价键结构的特性。这种结构我们称为这个分子的最稳定结构。 共振能( RE ) 就是总波函数的能量和最稳定结构的能量差:
式中 \(E^\textrm{tot}\) 表示总波函数的能量, \(E^\textrm{str}\) 表示最稳定结构的能量。由于 \(E^\textrm{str}\) 高于 \(E^\textrm{tot}\) , RE 是一个正值。如果一个分子的最稳定结构不止一个, \(E^\textrm{str}\) 一般为这几个结构构成的波函数。当然,在这几个最稳定结构中同样存在共振,同样也有共振能。
5.2. 如何计算共振能?
当我们了解了共振能的定义,我们就可以尝试计算共振能。一般情况下,我们需要先计算分子的总波函数以获得总能量 \(E^\textrm{tot}\) 和各个结构的权重,从而了解哪个/哪些结构是最重要的。
接下来,我们来考虑一个问题:
思考
在总波函数的计算中,我们已经获得了各个结构的哈密顿即能量,我们是否可以直接将结构的哈密顿作为结构的能量,一步到位算出共振能?
需要注意的是,总波函数中的结构能量是以总波函数的能量最低为目标进行自洽场优化的结果,此时结构波函数本身并不在最低点上。我们如果单独优化最稳定结构的波函数,会发现能量会进一步降低。而共振能的定义中,我们要求的是 最稳定结构的能量 ,因此我们需要单独针对最稳定结构进行优化,才能获得我们需要的 \(E^\textrm{str}\) 。如果我们直接将总波函数中最稳定结构的 Hamiltonian 抽出作为 \(E^\textrm{str}\) ,得到的 RE 值会偏高,此时我们得到的是垂直共振能( Vertical Resonance Energy,VRE ):
式中 \(E^\textrm{str}_v\) 表示最稳定结构的能量从总波函数的 Hamiltonian ,没有经过单独优化。VRE 可以作为 RE 的一个上限,是 RE 的一个比较好的估算值。
5.3. 共振能的具体应用
5.3.1. 电荷移动键
电荷移动键( Charge-Shift Bond,CSB )是一种非常特殊的化学键。传统的化学键一般可分为共价键和离子键两种。从波函数的角度看:共价键的主要成分是共价结构,离子键的主要成分是离子结构。从能量的角度看,共价键的键能主要有占主要成分的共价结构提供,离子键的键能由相应占主导的离子结构提供。而对于 CSB ,它在波函数上可以是共价或离子结构主导,但是主导的价键结构却无法提供足够的键能。CSB 的键能主要来自于多个价键结构间的共振。我们可以使用 相对共振能( Relative Resonance Energy, RRE ) 衡量共振能占键能的比例:
一般来说,当 \(RRE \ge 50\%\) ,我们可以认为化学键的形成主要依靠的是共振成键,因此 50% 可以作为化学键是否是 CSB 的一个经验判据。
CSB最典型的例子就是 F2 分子。传统认为,F2 是同核双原子分子,因此 F-F 之间的电子应该是共享为主,即 F-F 键应该是一个共价结构占主导的共价键。从波函数分析上,我们可以看到确实如此,价键计算似乎印证了我们的想法。然而,如果我们对共价结构单独进行价键计算,我们会发现:F-F 的共价结构能量竟然比解离时候的能量还要高!这意味着 F2 的共价结构是排斥的,不成键的。但是 F-F 键确实有 38.2 kcal/mol 的键能。那么这个键能是怎么来的呢?如 表 5.3.1 所示,我们发现,F2 的共振能远大于键能, RRE 达到了 200% 以上。显然,F2 的成键依赖于多个结构之间的共振,是一个 CSB 。
Methods |
Energies (a.u.) |
RE (kcal/mol) |
BDE (kcal/mol) |
RRE (%) |
|
|---|---|---|---|---|---|
Full |
Cov |
||||
VBSCF |
-198.751156 |
-198.674860 |
47.9 |
4.6 |
1041.3 |
BOVB |
-198.783180 |
-198.674860 |
68.0 |
24.7 |
275.0 |
VBCISD |
-198.972549 |
-198.871326 |
63.5 |
26.1 |
243.3 |
5.3.2. 芳香性的本质
我们以苯分子 C6 H6 为例,展示价键理论和共振论框架下探讨芳香性的本质。我们知道,芳香性是指共轭多烯烃,由于 \(\pi\) 电子的离域而产生的额外稳定性。这种离域共轭会造成共轭多烯烃原本的单-双键交替情况减弱,键长出现平均化。
苯分子是一种非常经典的芳香性物质。按照苯分子的分子式 C6 H6 ,苯分子应该是一种环己三烯,应该有明显的单-双键交替的情况。实际上,稳定态的苯分子是平面正六边形,6 个 C-C 键等长。这种显著的键长平均化预示着苯分子中的 \(\pi\) 电子具有强烈的离域性。以共振论的观点看,此时苯分子中有多个共振结构,共振的结果导致了键长的平均化,电子的离域,以及额外的稳定性。传统的分子轨道方法由于轨道的完全离域而无法计算电子定域的环己三烯,从而计算芳香性导致的稳定化能。而价键理论则可以很自然地进行计算。
我们将苯分子的 \(\pi\) 空间作为(6,6)的活性空间, \(\sigma\) 电子作为非活性空间,可以得到 5 个共价结构:
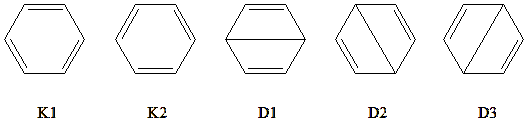
图 5.3.1 苯分子的5个共价结构
这 5 个价键结构可以分为2组:一组包含了 K1 和 K2 两个凯库勒结构,也就是环己三烯式的结构;一组包含了 D1-D3 三个杜瓦苯结构。从化学图像来看,我们很容易看到,两组结构在内部应该是简并的,即组内结构的权重应该是一样的;但是凯库勒结构由于没有长键,能量应该比杜瓦苯的结构更低,因此应该比杜瓦苯具有更大的权重。 STR=COV 的计算也符合我们的预期。
接下来,我们可以分别利用 2 个和 1 个凯库勒结构进行价键计算,得到相应结构的能量,以及相对于全共价结构的能量。从计算结果中可以看到,杜瓦苯结构并没有提供多少共振能,而凯库勒结构之间的共振则提供了绝大部分的共振能。由于共振能代表了更多结构带来的额外的稳定性,即稳定化能,因此,苯分子的芳香性的来源就是凯库勒结构之间的共振以及由此产生的共振能,如 表 5.3.2 和 表 5.3.3 所示。
Structure |
Coef. |
Weight |
|---|---|---|
K1 |
-0.40080 |
0.333 |
K2 |
-0.40080 |
0.333 |
D1 |
0.14218 |
0.111 |
D2 |
0.14218 |
0.111 |
D3 |
0.14218 |
0.111 |
Computation |
Energy (a.u.) |
RE (kcal/mol) |
|---|---|---|
5 Covalent Structures |
-230.604424 |
-- |
2 Kekulé Structures |
-230.599801 |
2.9 |
1 Kekulé Structure |
-230.556432 |
30.1 |