6. 激发态的计算与分析

到目前为止，我们关注的都是基态的计算。在实际科研任务中，分子不可能总是处于基态，人们的研究兴趣也不可能一直集中于分子的基态性质。因此，我们有必要在这一讲中简单讲一下如何进行激发态的计算。

6.1. MO 和 VB 中激发态的不同图像

在 MO 理论中，原子轨道经过线性组合得到分子轨道。分子轨道具有各自的能量，电子填充轨道遵循能量最低原理，即按照能量由低到高的顺序依次填充。如果遇到能量简并的情况，那就依据洪特规则，优先以自旋平行的方式填入各个简并轨道，然后再填满。按照这种法则得到的电子态，一般都是基态，因为此时空轨道的能量都比占据轨道高。如果电子填充轨道的时候没有遵循这些规则，比如填充简并轨道的时候没有遵循洪特规则，而是先填满了某个简并轨道，其它兼并轨道依然是未占据状态；或者没有遵循能量最低原理，优先填入了更高能量的轨道，更低能量的轨道反而是未占据或者未占满的状态，都会使得分子的能量升高。这种更高能级的状态就是所谓的 激发态 。这种状态是不稳定的，通常都是基态分子中的电子由于得到了某种形式的能量，比如光照，从而使电子跃迁到了更高能量的轨道或者组合形式而得到的。MO 理论中，分子的激发能可以粗略地用 Koopmann 原理进行估算，即

\[E_i^a = \varepsilon_a - \varepsilon_i\]

实际计算中，由于电子激发后，轨道会由于电子占据情况的改变而发生弛豫，实际的激发能还需要考虑轨道弛豫的影响，需要进行自洽场迭代优化。

在 VB 理论中，分子的波函数取决于两个方面：构成共振结构的轨道，以及共振结构间的线性组合。不同的轨道赋予了共振结构不同的物理含义和化学图像，不同的组合系数赋予了分子不同的性质和状态。组合系数通过求解久期方程得到。对于一个有 n 个结构的分子，久期方程对应于一个 n 阶广义本征方程，总共可以得到 n 个根。其中第一个根提供了最低的能量对应的组合形式。当轨道占据遵循能量最低原理时，第一个根提供的就是我们通常需要的基态。如果我们不选取第一个根，或者电子占据的不都是能量最低的轨道，我们得到的结构的组合就会发生变化，我们就得到了激发态。 我们从这里可以看到，VB理论的激发态计算有两个维度：轨道的选取和组合系数的变化。由于轨道的选取关系到共振结构具体的物理含义和化学图像，请参照我们的 节 2 和 节 3 内容。这一讲我们关注的是组合系数的变化对激发态的影响。

6.2. 如何在XMVB中计算激发态

6.2.1. 获取特定激发态

XMVB中提供了选取不同的久期方程的根的关键字 NSTATE=IROOT ，其中 IROOT 是一个非负整数，表示第几个激发态。 NSTATE=1 表示此时程序将选取第二个根来获得第一激发态的计算， NSTATE=2 表示第二激发态的计算，以此类推。 NSTATE=0 表示将进行基态（第零激发态）的计算，也是这个关键字的默认值。

我们先以H₂ 为例，看看 NSTATE=IROOT 的效果。默认情况下，XMVB 进行的是基态计算。对于H-H键长0.7 Å ，cc-pVDZ 基组的 HAO 计算，我们得到的能量是 -1.14386 a.u. ，3 个价键结构的系数和权重如下：

           ******  COEFFICIENTS OF STRUCTURES ******

    1      -0.84426638  ******    1-2
    2      -0.09228443  ******    1 1
    3      -0.09228443  ******    2 2


          ******  WEIGHTS OF STRUCTURES ******

    1       0.84327776  ******    1-2
    2       0.07836112  ******    1 1
    3       0.07836112  ******    2 2

可以看到，此时是共价结构占绝对主导的。如果我们加上了 NSTATE=1 ，最后的能量就变成了 -0.38420 a.u. ，相应的结构系数和权重也变成了：

           ******  COEFFICIENTS OF STRUCTURES ******

    1      -0.00000000  ******    1-2
    2       1.51521437  ******    1 1
    3      -1.51521436  ******    2 2


          ******  WEIGHTS OF STRUCTURES ******

    1       0.00000000  ******    1-2
    2       0.50000000  ******    1 1
    3       0.50000000  ******    2 2

可以看到，此时的波函数中已经没有了共价结构，离子结构的系数也从相同变成了相反。此时得到的就是第1激发态对应的结构系数。

接下来我们来看一个复杂一点的例子：O₂ 。O₂ 的三重态计算需要 12 个共振结构，单重态计算需要 10 个结构。三重态的 12 个结构见 图 6.2.1 。其中最重要的是 T1 和 T2 这两个结构。

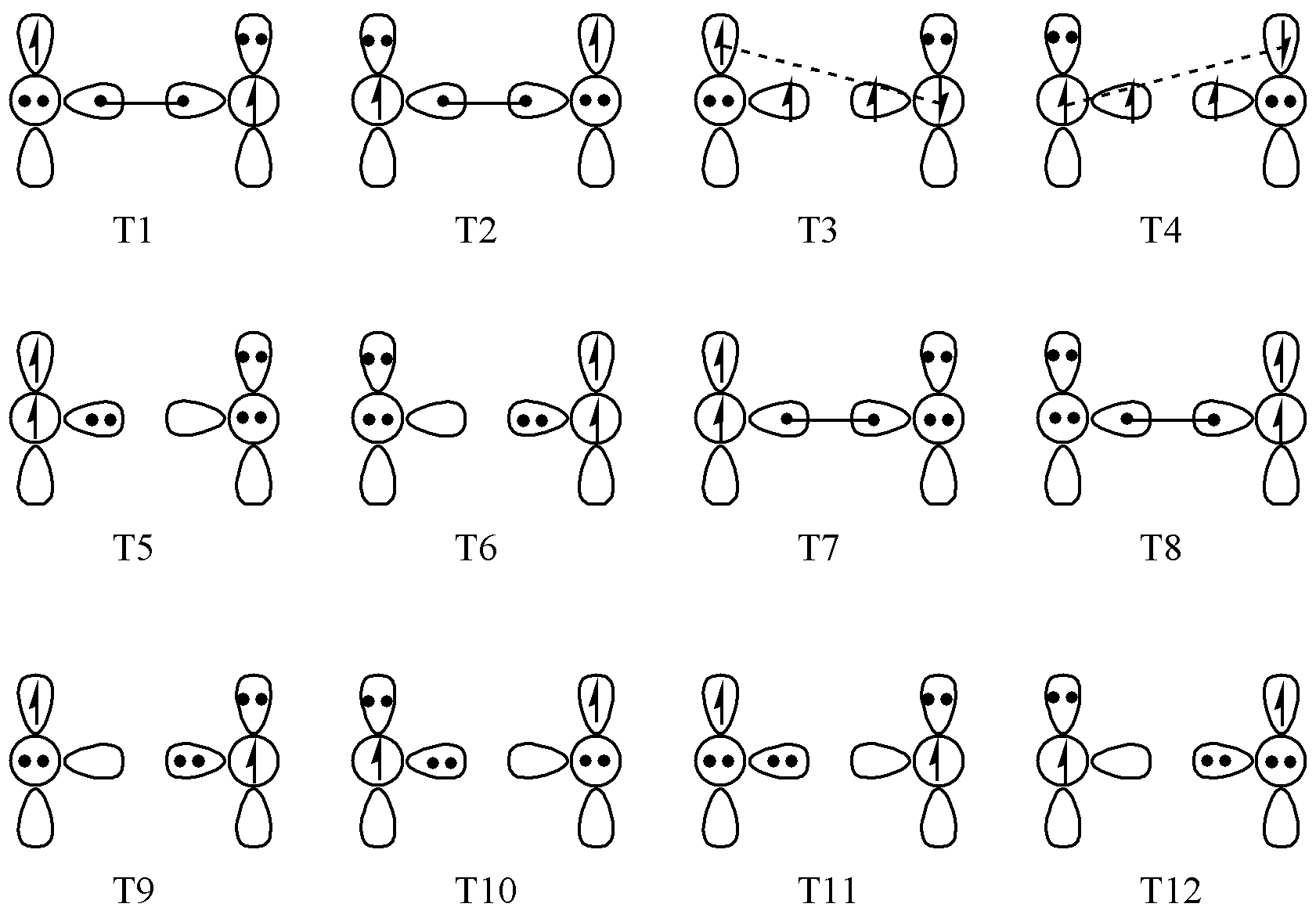
图 6.2.1 O₂ 三重态的12个价键结构

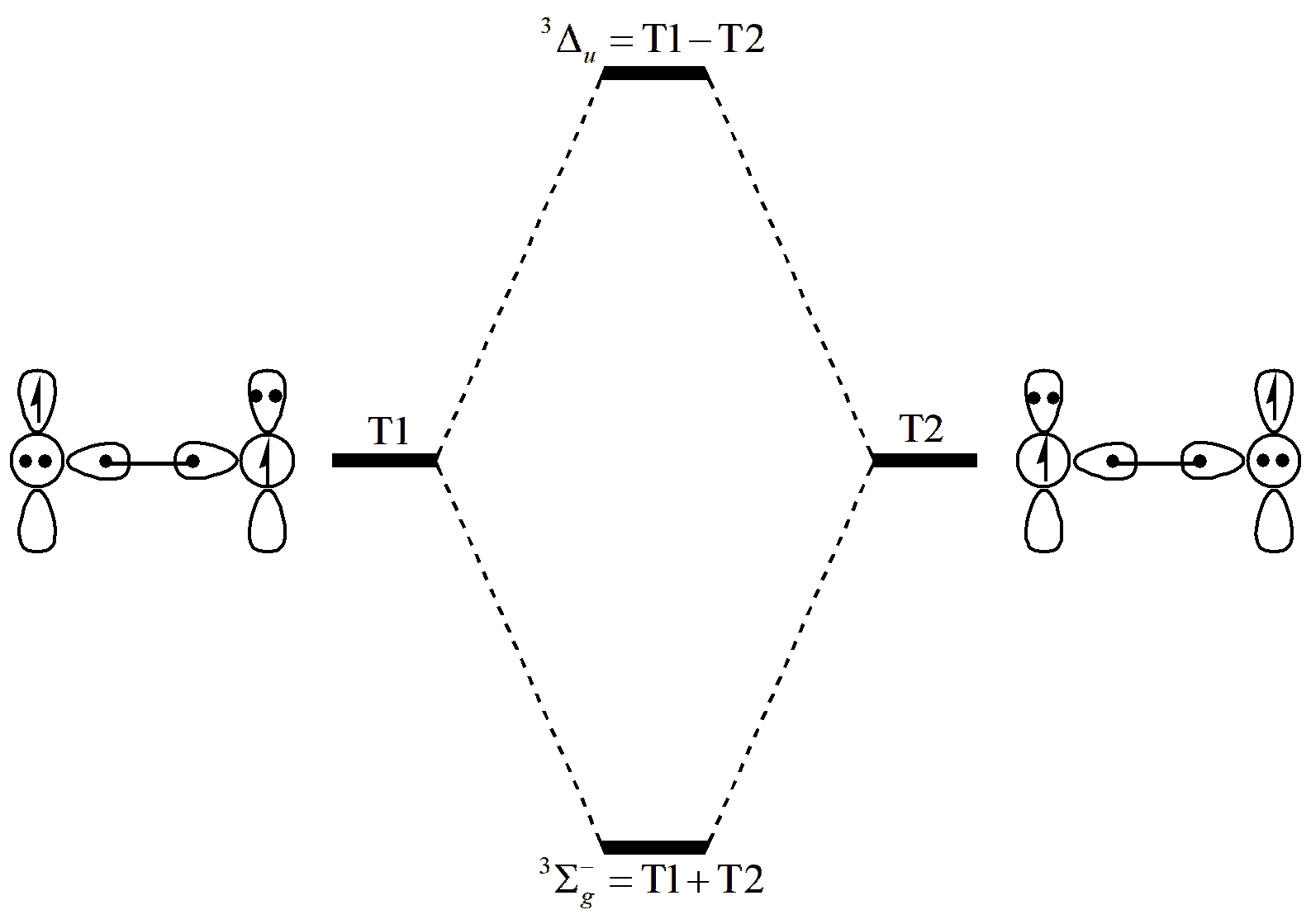
图 6.2.2 O₂ 三重态的基态和激发态

从 图 6.2.2 可以看到， T1 和 T2 的不同组合方式对应了不同的电子态。对于基态，两个结构的系数是相同的；对于激发态，组合系数是相反的。

为了得到三重态的激发态，我们可以利用 NSTATE=1 来计算三重态的第一激发态，如下：

O2 L-VBSCF
$ctrl
vbscf nstr=12 nao=6 nae=8 iscf=5 iprint=3
orbtyp=hao frgtyp=sao nmul=3 itmax=200 nstate=1
int=libcint basis=cc-pvdz
guess=read
$end
$str
1:4 7 7 10 10 5 6 8 9
1:4 8 8 9 9 5 6 7 10
1:4 7 7 10 10 8 9 5 6
1:4 8 8 9 9 7 10 5 6
1:4 7 7 9 9 5 6 8 10
1:4 8 8 10 10 5 6 7 9
1:4 8 8 10 10 5 5 7 9
1:4 7 7 9 9 6 6 8 10
1:4 8 8 9 9 5 5 7 10
1:4 7 7 10 10 6 6 8 9
1:4 7 7 10 10 5 5 8 9
1:4 8 8 9 9 6 6 7 10
$end
$frag
1*6
spzdxxdyydzzfzzzfxxzfyyz 1
spzdxxdyydzzfzzzfxxzfyyz 2
pxdxzfxxxfxyyfxzz 1
pxdxzfxxxfxyyfxzz 2
pydyzfyyyfxxyfyzz 1
pydyzfyyyfxxyfyzz 2
$end
$orb
1*10
1
2
1
2
1
2
3
4
5
6
$end
$geo
O 0.0 0.0 0.0
O 0.0 0.0 1.2
$end
$gus
    8    8    8    8    8    8    3    3    3    3
 1.0019774038    1   0.0065168066    2   0.0001788772    3   0.0010309980    6
-0.0003633198    9  -0.0027414664   10  -0.0030686413   13  -0.0030026561   15
 1.0021643892   16   0.0072505362   17   0.0002382456   18  -0.0011188449   21
 0.0003834680   24  -0.0030102480   25  -0.0031503232   28  -0.0032525782   30
 0.0982223750    1  -0.2504910231    2  -0.8206750714    3  -0.0401288970    6
-0.3250457745    9   0.0663093980   10   0.0645475585   13  -0.0255293114   15
 0.1023941578   16  -0.2356452123   17  -0.8258612653   18   0.0419646005   21
 0.3491578062   24   0.0683659578   25   0.0684486346   28  -0.0278018600   30
-0.0534466425    1  -0.2957625003    2  -0.0041914149    3   0.2677956458    6
 0.7578794938    9  -0.0782023209   10  -0.0786400588   13   0.0255903120   15
-0.0521455763   16  -0.3057336084   17  -0.0199773005   18  -0.2554552086   21
-0.7557006120   24  -0.0788914259   25  -0.0791889215   28   0.0231651215   30
 0.5315910156    4   0.6213802169    7   0.0117253831   12
 0.5179245322   19   0.6342323659   22  -0.0135520711   27
 0.5280659286    5   0.6247144659    8   0.0122018946   14
 0.5244186959   20   0.6281355341   23  -0.0136783062   29
$end

相对于基态的计算，激发态计算的文件仅仅多了一个 NSTATE 关键字。我们可以将 NSTATE=1 去掉实现基态的计算。最终，我们得到了 表 6.2.1 的计算结果：

表 6.2.1 基态和激发态下O₂ 三重态的价键波函数

结构	基态		激发态
	系数	权重	系数	权重
T1	-0.343	0.220	-0.492	0.327
T2	-0.343	0.220	0.492	0.327
T3	-0.018	0.000	-0.036	0.001
T4	0.018	0.000	-0.036	0.001
T5	0.166	0.073	0.000	0.000
T6	0.166	0.073	0.000	0.000
T7	0.178	0.091	0.000	0.000
T8	0.178	0.091	0.000	0.000
T9	-0.125	0.058	-0.180	0.086
T10	-0.125	0.058	0.180	0.086
T11	-0.125	0.058	-0.180	0.086
T12	-0.125	0.058	0.180	0.086

从计算结果中可以看到， T1 和 T2 两个结构的系数在基态和激发态中的系数组合确实发生了变化。同时我们可以看到，无论从系数还是权重来看，激发态相对于基态更集中于 T1 和 T2 ，其它结构在总波函数中的贡献均有下降。O₂ 三重态的第一激发态更主要由 T1 和 T2 两个结构组成。

6.2.2. 态平均计算

我们在进行激发态计算的时候，常常会使用“态平均”。所谓态平均，就是我们不是优化某一个特定的电子态，而是将数个我们感兴趣的电子态能量按一定的权重进行组合，利用自洽场迭代优化，使得组合后的总能量达到最低：

\[E = \sum_i{w_iE_i}\]

其中 \(E\) 为总能量， \(E_i\) 为参与态平均的某个态的能量。 \(w_i\) 为事先拟定的权重，在整个迭代优化过程中保持不变。

在XMVB中，我们可以利用 WSTATE 关键字进行态平均计算。WSTATE 关键字的语法为：

WSTAE( start )= \(w_{\textrm{start}}\), \(w_\textrm{start+1}\), ...

其中括号中的 start 表示起始态的编号，基态为1，第一激发态为2，以此类推。等号后以逗号为间隔，可以输入多个对应的权重。例如：

WSTATE(1)=0.4,0.6

表示进行一个两态的态平均计算，其中基态的权重为 0.4 ，第一激发态的权重为 0.6 。WSTATE 关键词也可以多个叠加使用，比如：

WSTATE(1)=0.5,0.5 WSTATE(5)=0.4,0.6

表示态平均计算涉及 4 个态：基态（权重 0.5 ），第一激发态（权重 0.5 ），第四激发态（权重 0.4 ）和第五激发态（权重 0.6 ）。需要注意的是，此时权重之和已经大于 1 了。XMVB 会自动将总权重进行归一，因此上述关键词等同于：

WSTATE(1)=0.25,0.25 WSTATE(5)=0.2,0.3

用户只需要关心不同态之间权重的比值即可。WSTATE 的默认值为

WSTATE(1)=1.0,0.0,0.0, ...

即只进行基态的优化。态平均计算可用于 VBSCF 和 BOVB 计算。 我们以 H₂ 为例，进行一个态平均计算。这个算例涉及基态和第一激发态，对应的权重分别为 0.7 和 0.3 。输入文件如下所示：

H2 State average
$ctrl
vbscf
str=full nao=2 nae=2 iscf=5
orbtyp=hao frgtyp=atom
int=libcint basis=cc-pvdz
wstate(1)=0.7,0.3
$end
$orb
1*2
1
2
$end
$geo
H 0.0 0.0 0.0
H 0.0 0.0 0.74
$end

在输出文件中，我们可以看到如下信息，提示用户这是一个态平均计算：

  Stat average computation with folllowing states and weights:

   STATE     WEIGHT
     1       0.700
     2       0.300

最终，除了总能量以外，XMVB 还会输出态平均中每个涉及的电子态的能量，结构系数及权重信息，如下所示（以基态信息为例）：

         STATE:     1
         ENERGY:      -1.13344128
         WEIGHT:       0.70000000

         ******  COEFFICIENTS OF STRUCTURES ******

  1      -0.90250405  ******    1-2
  2       0.05647560  ******    1 1
  3       0.05647560  ******    2 2


        ******  WEIGHTS OF STRUCTURES ******

  1       0.90219477  ******    1-2
  2       0.04890261  ******    1 1
  3       0.04890261  ******    2 2