5. Resonance Energy

In the previous lecture, we learned how to calculate bond dissociation energies. Bond dissociation energy is a well-defined physical quantity, and it can be readily measured in experiments with specific molecular examples. In this lecture, we will introduce a physical quantity that is very important in valence bond theory but difficult to observe directly in reality: the resonance energy.

5.1. Definition of Resonance Energy

Resonance energy (RE) was introduced along with Linus Pauling’s resonance theory. In resonance theory, the stable structure of a molecule is formed by the resonance of multiple valence bond (VB) structures. From the wavefunction perspective, the total wavefunction of a molecule can be expressed as a linear combination of individual VB wavefunctions. The energies of individual valence bond structures are not identical. One or a few of them have the lowest energies and thus carry the largest weights in the total molecular wavefunction. Consequently, the molecular structure more prominently reflects the characteristics of these lowest-energy structures. Such structures are referred to as the most stable structures of the molecule. The resonance energy (RE) is defined as the difference between the total wavefunction energy and the energy of the most stable structure:

\[RE = E^\textrm{str} - E^\textrm{tot}\]

Here, \(E^\textrm{tot}\)is the energy of the total wavefunction and \(E^\textrm{str}\)is the energy of the most stable structure. Since \(E^\textrm{tot}\)is always lower than \(E^\textrm{str}\), RE is a positive by definition. If a molecule has more than one most stable structure, \(E^\textrm{str}\)usually refers to the wavefunction composed of these few structures. Naturally, resonance also exists among them, and there will be resonance energy as well.

5.2. How to Calculate Resonance Energy?

Once we understand the definition of resonance energy, we can attempt to calculate it. Generally, we first compute the total wavefunction of the molecule to obtain the total energy \(E^\textrm{tot}\)and the weights of the individual structures, thereby identifying which structure(s) are most important.

Now let us consider a question:

Consider

In calculating the total wavefunction, we already obtain the Hamiltonian and energy of each structure. Can we directly take the Hamiltonian of a structure as its energy and thus compute the resonance energy in one step?

It is important to note that the structure energies appearing in the total wavefunction are the results of self-consistent field (SCF) optimization aimed at minimizing the total wavefunction energy. At this stage, the individual structure wavefunctions themselves are not at their own minima. If we optimize the wavefunction of the most stable structure separately, its energy will decrease further. In the definition of resonance energy, what we require is the energy of the most stable structure. Therefore, we need to perform a separate optimization for the most stable structure in order to obtain the desired \(E^\textrm{str}\). If we directly extract the Hamiltonian of the most stable structure from the total wave function as \(E^\textrm{str}\), the resulting RE value will be overestimated; in this case, what we obtain is the vertical resonance energy (VRE):

\[VRE = E^\textrm{str}_v - E^\textrm{tot}\]

Here, \(E^\textrm{str}_v\)refers to the energy of the most stable structure taken from the Hamiltonian of the total wavefunction without separate optimization. VRE serves as an upper bound to RE and is a useful estimate.

5.3. Applications of Resonance Energy

5.3.1. Charge-Shift Bond

The charge-shift bond (CSB) is a very special type of chemical bond. Traditionally, chemical bonds are divided into covalent bonds and ionic bonds. From a wavefunction perspective, covalent bonds are dominated by covalent structures, and ionic bonds are dominated by ionic structures. From an energy perspective, the bond energy of a covalent bond mainly comes from the dominant covalent structure, and that of an ionic bond comes from the dominant ionic structure. For a CSB, however, the wavefunction may be dominated by either covalent or ionic structures, yet the dominant structure alone cannot provide sufficient bond energy. Instead, the bond energy of a CSB mainly arises from resonance among multiple VB structures. We can use the relative resonance energy (RRE) to quantify the fraction of bond energy contributed by resonance:

\[RRE = \frac{RE}{BDE} \times 100\%\]

In general, when \(RRE \ge 50\%\), we can consider the bond to be primarily stabilized through resonance, and 50% can serve as an empirical criterion for identifying a CSB.

The most typical example of a CSB is the F₂ molecule. Traditionally, F₂ is regarded as a homonuclear diatomic molecule, so the F–F electrons should be primarily shared, making the F–F bond a covalent bond dominated by a covalent structure. From wavefunction analysis, this seems to be correct, and VB calculations appear to confirm this. However, if we perform a VB calculation on the covalent structure alone, we find that the covalent structure energy of F–F is actually higher than the energy at dissociation! This means that the covalent structure of F₂ is repulsive and non-bonding. Yet, the F–F bond has a bond dissociation energy of 38.2 kcal/mol. Where does this bond energy come from? As shown in Table 5.3.1, we find that the resonance energy of F₂ is much greater than its bond energy, with RRE exceeding 200%. Clearly, the bonding in F₂ relies heavily on resonance among multiple structures, making it a CSB.

Table 5.3.1 Calculation results for F₂ under different methods

Methods	Energies (a.u.)		RE (kcal/mol)	BDE (kcal/mol)	RRE (%)
	Full	Cov
VBSCF	-198.751156	-198.674860	47.9	4.6	1041.3
BOVB	-198.783180	-198.674860	68.0	24.7	275.0
VBCISD	-198.972549	-198.871326	63.5	26.1	243.3

5.3.2. The Essence of Aromaticity

Let us take benzene ( C₆ H₆ ) as an example to explore the essence of aromaticity within the framework of valence bond theory and resonance theory. Aromaticity refers to the extra stability of conjugated polyenes due to the delocalization of \(\pi\)electrons. This delocalization reduces the original single–double bond alternation in conjugated polyenes and results in bond length equalization.

Benzene is a classic example of an aromatic compound. From its molecular formula C₆ H₆, benzene could be considered a cyclohexatriene, and one might expect alternating single and double bonds. In reality, however, the stable form of benzene is a planar regular hexagon with six equivalent C–C bonds. This strong bond-length equalization indicates significant delocalization of the \(\pi\)electrons. From the resonance perspective, benzene contains multiple resonance structures. Resonance among these structures results in bond length equalization, electron delocalization, and additional stabilization. Traditional molecular orbital methods, because of their fully delocalized orbitals, cannot compute the stabilization energy from localized cyclohexatriene structures, making it difficult to quantify aromatic stabilization. Valence bond theory, however, can naturally perform such calculations.

By taking the \(\pi\) space of benzene as an active space (6,6) and treating the \(\sigma\)electrons as inactive, we obtain five covalent structures:

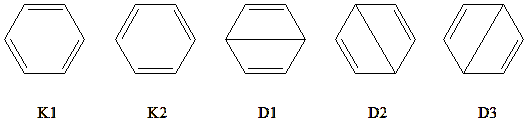
Fig. 5.3.1 Benzene’s five covalent structures

These five VB structures can be grouped into two sets: one consisting of the two Kekulé structures (K1 and K2), i.e., cyclohexatriene-like structures, and another consisting of the three Dewar benzene structures (D1–D3). From a chemical viewpoint, it is easy to see that the structures within each group should be degenerate and carry equal weights. Moreover, the Kekulé structures, which lack long bonds, should be lower in energy and thus have higher weights than the Dewar structures. Calculations with STR=COV confirm this expectation.

Next, we can carry out VB calculations using two Kekulé structures and then only one Kekulé structure, obtaining their energies and resonance energies relative to the full five-structure calculation. From the results, we see that the Dewar structures contribute very little resonance energy, while most of the resonance energy comes from resonance between the two Kekulé structures. Since resonance energy represents additional stabilization from the inclusion of more structures, the aromaticity of benzene arises primarily from the resonance between the Kekulé structures and the associated resonance energy, as shown in Table 5.3.2 and Table 5.3.3.

Table 5.3.2 Coefficients and weights of benzene’s structures

Structure	Coef.	Weight
K1	-0.40080	0.333
K2	-0.40080	0.333
D1	0.14218	0.111
D2	0.14218	0.111
D3	0.14218	0.111

Table 5.3.3 Energies and resonance energies for different numbers of structures

Computation	Energy (a.u.)	RE (kcal/mol)
5 Covalent Structures	-230.604424	–
2 Kekulé Structures	-230.599801	2.9
1 Kekulé Structure	-230.556432	30.1