8. Valence Bond Theory and Diabatic States
In the previous lecture we introduced how to compute and analyze chemical reaction processes using valence bond theory and the XMVB program. In practical calculations, many chemical processes involve electron transfer, such as electron transport, photophysical processes, and photochemical processes. In such areas of computation, the concept of diabatic states often arises. In this lecture, we will briefly introduce the application of valence bond theory to the calculation of diabatic states.
8.1. What is an adiabatic state? What is a diabatic state?
“Diabatic state” is a concept corresponding to the adiabatic state. To understand diabatic states, we must first understand adiabatic states. Simply put, an adiabatic state is an eigenstate obtained by solving the electronic Schrödinger equation of the system under the Born–Oppenheimer approximation. The electronic states we usually refer to are adiabatic states, and the various potential energy curves correspond to the energies of adiabatic states.
In general, adiabatic curves do not cross. However, in studies involving electron transfer processes, different adiabatic states become degenerate near the regions where electron transfer occurs. At such points, the energies of two adiabatic states become very close or even identical, and their adiabatic potential energy curves approach each other or even intersect, forming a “conical intersection” region. At this point, the Born–Oppenheimer approximation breaks down, and certain physical quantities exhibit abrupt changes near the conical intersection, creating singularities. This presents challenges for theoretical research.
To overcome these difficulties, researchers take the nearly degenerate or degenerate adiabatic states as a basis and perform a certain transformation to recombine the adiabatic states into a set of new wavefunctions. In this new representation, the singularities disappear and the variation of physical quantities becomes smooth and continuous. These recombined wavefunctions are called diabatic states.
8.2. Why use valence bond theory to compute diabatic states?
From Section 8.1, we see that adiabatic states are strictly defined mathematically, while diabatic states are not. Typically, one first computes adiabatic states near the conical intersection region, and then applies a transformation matrix to recombine them into diabatic states. This transformation is not unique, so the resulting diabatic states are also not unique. Moreover, since molecular orbital (MO) or density functional theory (DFT) wavefunctions are usually employed, the use of delocalized orthogonal orbitals often obscures the chemical picture of the diabatic states.
Valence bond (VB) wavefunctions, however, are naturally multiconfigurational. Each adiabatic state corresponds to a certain combination of VB structures. Each VB structure corresponds to a specific electronic occupation, and transformations between VB structures can describe electron transfer processes. Thus, VB structures can serve as the foundation for constructing diabatic wavefunctions. Using VB wavefunctions to compute and describe diabatic states is not only feasible, but also provides a clear chemical picture for diabatic states.
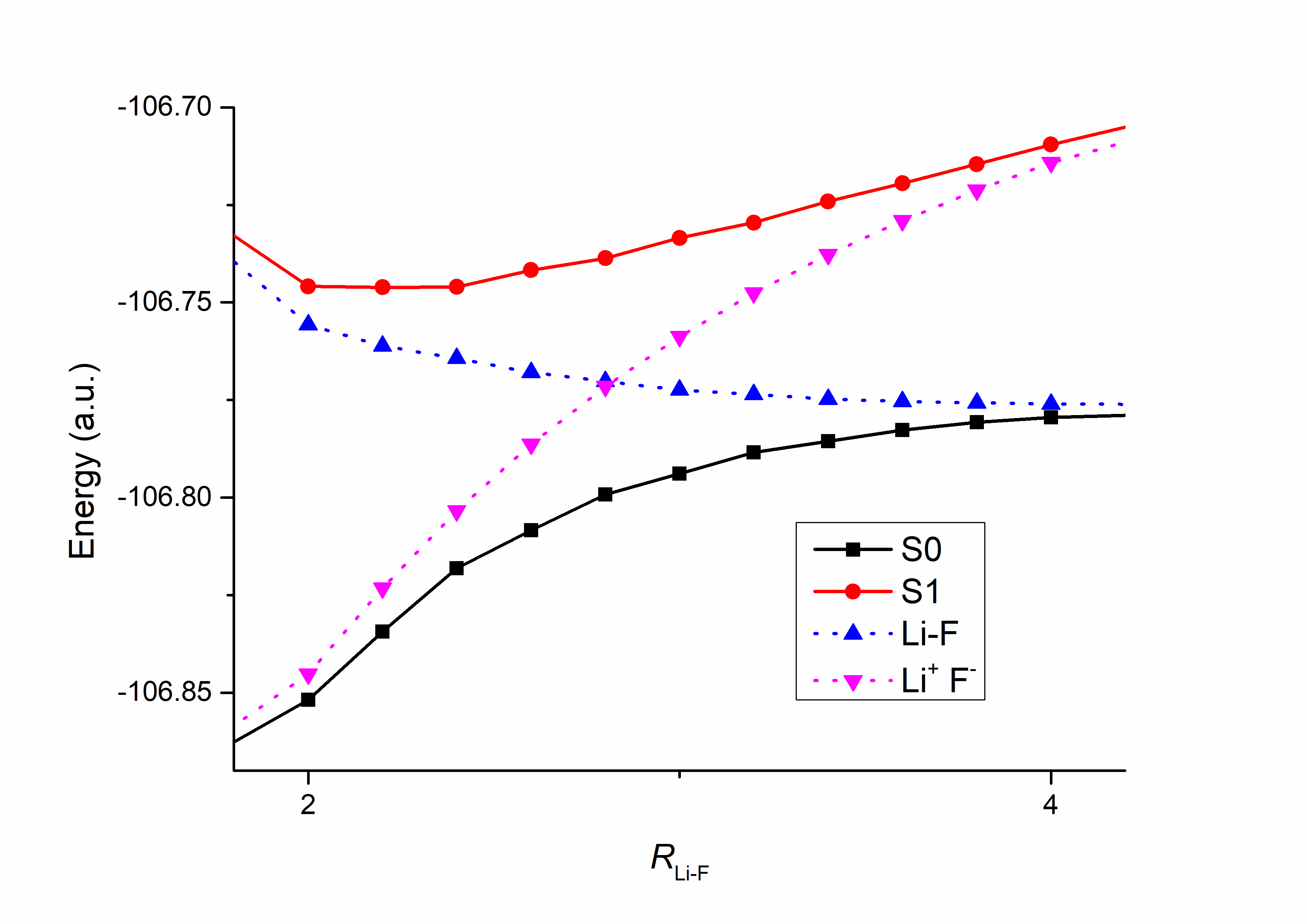
Fig. 8.2.1 Dissociation curve of LiF (partial)
Fig. 8.2.1 shows a detailed segment of the LiF potential energy curves between 2.0–4.0 Å. S0 and S1 are two adiabatic states; Li–F and Li+ F- respectively denote the covalent structure and the ionic structure in the Li⁺F⁻ form. We can clearly see that as dissociation proceeds, the main component of the ground state S₀ gradually changes from ionic to covalent, meaning that an electron is gradually transferred from the F atom to the Li atom. This result emerges naturally, without any artificial manipulation.
8.3. How to compute diabatic states in XMVB?
It is important to note that although a VB structure can well represent a diabatic state, a diabatic state is not the same as a single VB structure. To obtain diabatic states, we must recombine adiabatic states into diabatic states, a process called diabatization. Currently, most diabatization methods are MO-based. The research group of Prof. Peifeng Su at Xiamen University has developed a VB-based ab initio diabatization method, VBCAD, which performs black-box VB diabatization and yields diabatic states based on VB structures. VBCAD has been implemented in XMVB, and users can invoke it using the keyword VBCAD. At present, VBCAD supports only two-state diabatization.
VBCAD is based on state-averaged calculations (see Section 6.2.2 ). Users can perform state-averaged VB calculations and then add VBCAD keyword to obtain diabatic states. For example, for LiF, the VBCAD input file is as follows (the $GUS part is omitted):
1LiF
2$CTRL
3VBSCF
4STR=FULL NAO=2 NAE=2 ISCF=5 IPRINT=3
5ORBTYP=HAO FRGTYP=SAO INT=LIBCINT BASIS=CC-PVDZ
6WSTATE(1)=0.5,0.5 GUESS=READ VBCAD
7$END
8$FRAG
91*4
10SPZDXXDYYDZZ 1
11SPZDXXDYYDZZ 2
12PXDXZ 2
13PYDYZ 2
14$END
15$ORB
161*7
171
182
192
203
214
221
232
24$END
25$GEO
26Li 0.0 0.0 0.0
27F 0.0 0.0 1.5
28$END
In the output file, user will see a section like this:
1 ++ VBCAD Diabatic States Output:
2 -----------------------------
3 …
4
5
6 ++ Adiabatic States Output:
7 ------------------------
The VBCAD results are located in between. For LiF, we can obtain two diabatic states, as follows:
1 VBCAD DIABATIC STATE: 1
2 VBCAD DIABATIC ENERGY: -106.714561
3
4
5 ****** COEFFICIENTS OF STRUCTURES ******
6
7 1 1.00164 ***** 1:5 6-7
8 2 -0.01689 ***** 1:5 6 6
9 3 -0.02551 ***** 1:5 7 7
10
11 CC Weights
12
13 1 1.00117 ***** 1:5 6-7
14 2 -0.00055 ***** 1:5 6 6
15 3 -0.00062 ***** 1:5 7 7
And
1 VBCAD DIABATIC STATE: 2
2 VBCAD DIABATIC ENERGY: -106.877821
3
4
5 ****** COEFFICIENTS OF STRUCTURES ******
6
7 1 0.02420 ***** 1:5 6-7
8 2 0.00047 ***** 1:5 6 6
9 3 -1.00091 ***** 1:5 7 7
10
11 CC Weights
12
13 1 -0.00062 ***** 1:5 6-7
14 2 0.00000 ***** 1:5 6 6
15 3 1.00062 ***** 1:5 7 7
We can see that the first diabatic state corresponds essentially to the covalent Li–F structure, while the second diabatic state corresponds essentially to the ionic Li+ F- structure.